Sistem pertidaksamaan linear dua variabel

sumber: https://www.rumahnumerasi.com

SISTEM PERTIDAKSAMAAN LINEAR DUA VARIABEL

A. Pertidaksamaan Linear Dua Variabel (PtdLDV)

Pertidaksamaan linear adalah kalimat terbuka yang dihubungkan dengan tanda ketidaksamaan dan mengandung variabel berpangkat satu.

Bentuk umum pertidaksamaan linear adalah :

$ax + by > c$

$ax + by < c$

$ax + by ≥ c$

$ax + by ≤ c$

Dengan :

$x$ dan $y$ sebagai variabel

$a$, $b$, dan $c$ adalah konstanta

Langkah-langkah untuk menyelesaikan pertidaksamaan linear:

1. Nyatakan pertidaksamaan linear sebagai persamaan linear dalam bentuk

          $ax + by = c$ (garis pembatas)

1. Tentukan titik potong garis $ax + by = c$ dengan sumbu $x$ dan sumbu $y$
2. Tarik garis lurus yang menghubungkan kedua titik potong tersebut. Jika pertidaksamaan dihubungkan dengan tanda $≥$ dan $≤$, maka garis lukis tidak putus-putus, sedangkan jika pertidaksamaan dihubungkan dengan tanda $>$ atau $<$, maka garis dilukis putus-putus.
3. Tentukan sembarang titik $(x, y)$ substitusikan ke pertidaksamaan. Jika pertidaksamaan bernilai benar, maka daeerah tersebut merupakan daerah penyelesaian, sebaliknya jika pertidaksamaan bernilai salah, maka daerah tersebut bukan merupakan daerah penyelesaian.
4. Arsirlah daerah yang memenuhi, sehingga daerah himpunan penyelesaiannya adalahdaerah yang diarsir.

Catatan:

• Tanda pertidaksamaan $≥$ mengisyaratkan daerah penyelesaian berada di sebelah kanan atas garis.
• Tanda pertidaksamaan $≤$ mengisyaratkan daerah penyelesaian berada di sebelah kiri bawah garis.

Contoh Soal:

Tunjukkan daerah penyelesaian PtdLDV berikut!

1. $3x + 2y ≥ 12$

2. $2x + 3y > 6$

3. $−x + 2y < 2$

4. $3x − y ≤ 6$

Penyelesaian:

1. $3x + 2y ≥ 12$

➢ Persamaan garis pembatas $3x + 2y = 12$

➢ Tentukan titik potong terhadap sumbu $x$ dan sumbu $y$

Titik potong sumbu $x$, maka $y = 0$

Sehingga:

$3x + 2y = 12$

$3x + 2(0) = 12$

$3x + 0 = 12$

$3x = 12$

$x = 4$

Jadi, titik potong terhdap sumbu $x$ adalah $(4,0)$

➢ Tentukan titik potong terhadap sumbu $x$ dan sumbu $y$

Titik potong sumbu $y$, maka $x = 0$

Sehingga:

$3x + 2y = 12$

$3(0) + 2y = 12$

$0 + 2y = 12$

$2y = 12$

$y = 6$

Jadi, titik potong terhdap sumbu $y$ adalah $(0,6)$

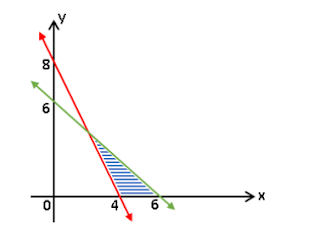
➢ Gambar garis $3x + 2y = 12$ melalui titik $(4,0)$ dan $(0,6)$ sebagai berikut.

➢ Ambil sembarang titik, misalnya $(0,0)$, substitusikan ke persamaan :

$3x + 2y ≥ 12$

$3(0) + 2(0) ≥ 12$

$0 ≥ 12$ (Tidak Mungkin)

Berarti daerah tempat titik $(0,0)$ bukan merupakan terletak di daerah penyelesaian.

➢ Arsirlah daerah yang memenuhi pertidaksamaan tersebut.

2. $2x + 3y > 6$

➢ Garis pembatas $2x + 3y = 6$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	3
y	2	0
(x,y)	(0,2)	(3,0)

➢ Gambar garis $2x + 3y = 6$ melalui titik $(0,2)$ dan $(3,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

3. $−x + 2y < 2$

➢ Garis pembatas $−x + 2y = 2$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	-2
y	1	0
(x,y)	(0,1)	(-2,0)

➢ Gambar garis $−x + 2y = 2$ melalui titik $(0,1)$ dan $(-2,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

4. $3x − y ≤ 6$

➢ Garis pembatas $3x − y = 6$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	2
y	-6	0
(x,y)	(0,-6)	(2,0)

➢ Gambar garis $3x − y = 6$ melalui titik $(0,-6)$ dan $(2,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

B. Sistem Pertidaksamaan Linear Dua Variabel (SPtdLDV)

Sistem pertidaksamaan linear dua variabel adalah gabungan dari dua atau lebih pertidaksamaan linear dengan dua variabel.

Contoh soal:

Tentukan daerah penyelesaian dari sistem pertidaksamaan linear dengan dua variabel berikut.

1. $2x + y ≤ 4$

    $2x + 3y ≤ 6$

    $x ≥ 0$

    $y ≥ 0$

2. $x + y ≤ 6$

    $2x + y ≥ 8$

    $x ≥ 0$

    $y ≥ 0$

3. $x + 2y ≥ 6$

    $3x + y ≤ 9$

    $x ≥ 0$

    $y ≥ 0$

4. $4x + 3y ≥ 12$

    $2x + 5y ≥ 10$

    $x ≥ 0$

    $y ≥ 0$

Jawaban:

1. $2x + y ≤ 4$

    $2x + 3y ≤ 6$

    $x ≥ 0$

    $y ≥ 0$

Penyelesaian:

➢ Garis pembatas $2x + y = 4$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	2
y	4	0
(x,y)	(0,4)	(2,0)

➢ Gambar garis $2x + y = 4$ melalui titik $(0,4)$ dan $(2,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

➢ Garis pembatas $2x + 3y = 6$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	3
y	2	0
(x,y)	(0,2)	(3,0)

➢ Gambar garis $2x + 3y = 6$ melalui titik $(0,2)$ dan $(3,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

2. $x + y ≤ 6$

    $2x + y ≥ 8$

    $x ≥ 0$

    $y ≥  0$

Penyelesaian:

➢ Garis pembatas $x + y = 6$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	6
y	6	0
(x,y)	(0,6)	(6,0)

➢ Gambar garis $x + y = 6$ melalui titik $(0,6)$ dan $(6,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

➢ Garis pembatas $2x + y = 8$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	4
y	8	0
(x,y)	(0,8)	(4,0)

➢ Gambar garis $2x + y = 8$ melalui titik $(0,8)$ dan $(4,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

3. $x + 2y ≥ 6$

    $3x + y ≤ 9$

    $x ≥ 0$

    $y ≥ 0$

Penyelesaian:

➢ Garis pembatas $x + 2y = 6$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	6
y	3	0
(x,y)	(0,3)	(6,0)

➢ Gambar garis $x + 2y = 6$ melalui titik $(0,3)$ dan $(6,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

➢ Garis pembatas $3x + y = 9$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	3
y	9	0
(x,y)	(0,9)	(3,0)

➢ Gambar garis $3x + y = 9$ melalui titik $(0,9)$ dan $(3,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

4. $4x + 3y ≥ 12$

    $2x + 5y ≥ 10$

    $x ≥ 0$

    $y ≥ 0$

Penyelesaian:

➢ Garis pembatas $4x + 3y = 12$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	3
y	4	0
(x,y)	(0,4)	(3,0)

➢ Gambar garis $4x + 3y = 12$ melalui titik $(0,4)$ dan $(3,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

➢ Garis pembatas $2x + 5y = 10$

➢ Titik potong sumbu $x$ dan sumbu $y$

x	0	5
y	2	0
(x,y)	(0,2)	(5,0)

➢ Gambar garis $2x + 5y = 10$ melalui titik $(0,2)$ dan $(5,0)$

➢ Arsir daerah yang memenuhi daerah penyelesaian pertidaksamaan linear

Semoga Bermanfaat

Selamat Belajar

Salam Matematika

sumber : rumahnumerasi.com