Luas Permukaan Benda Putar

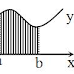
Salah satu aplikasi integral tak tentu adalah untuk menghitung luas. Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva, di bawah kurva, di atas sumbu $x$ ataupun di bawah sumbu $x$. Untuk itulah maka kita perlu memahami gambar kurva.

Untuk lebih jelasnya perhatikan kasus-kasus berikut

Jika kurva berada di bawah sumbu x maka metodanya adalah

Jika di antara dua kurva maka caranya sebagai berikut

Contoh soal 1

Tentukan luas daerah yang diarsir !

Jawab :

$L=\int_{0}^{2}6x^2dx$

     $=\frac{6}{2+1}x^{2+1}$

     $=\frac{6}{3}x^3$

     $=2x^3$

     $=2(2^3-0^3)$

     $=2(8)$

     $=16$

Contoh soal 2 :

Carilah luas daerah yang diarsir !Luas daerah di bawah sumbu x

Jawab :

$L=-\int_{1}^{3}3x^3-12x+9dx$

     $=\int_{1}^{3}-3x^3+12x-9dx$

     $=-\frac{3}{2+1}x^{3+1}+\frac{12}{1+1}x^{1+1}-9x$

     $=-x^3+6x^2-9x$

     $=(-3^3+6(3^2)-9(3))-(-1^3+6(1^2)-9(1))$

     $=((-27)+54-27)-((-1)+6-9)$

     $=0-(-4)$

     $=4$

Contoh Soal 3 :

Luas daerah yang diarsir adalah …

Jawab

$L=\int_{-1}^{1}(12-3x^2-(6-3x))dx$

    $=\int_{-1}^{1}(6+3x-3x^2)dx$

    $=6x+\frac{3}{1+1}x^{1+1}-\frac{3}{2+1}x^{2+1}$

    $=6x+\frac{3}{2}x^2-x^3$

    $=(6(1)+\frac{3}{2}1^2-1^3)-((6(-1)+\frac{3}{2}(-1^2)-(-1^3))$

    $=(6+\frac{3}{2}1-1)-((-6)+\frac{3}{2}1+1)$

    $=(6+\frac{3}{2}-1)-((-6_+\frac{3}{2}+1)$

    $=6+6+\frac{3}{2}-\frac{3}{2}-1-1$

    $=10$

Contoh Soal 4 :

Tentukan luas daerah yang diarsir berikut

Jawab :

misalkan persamaan garis kita tulis menjadi $f(x) = 2x – 17$ dan parabola menjadi $g(x) = x^2 – 25$. Pada bagian yang diarsir, kurva $f(x)$ lebih di atas dibandingkan dengan kurva $g(x)$

Maka luas daerah di atas bisa dinyatakan dengan

$L=\int_{-2}^{4}(2x-17-(x^2-25))dx$

    $=\int_{-2}^{4}(-x^2+2x+8)dx$

    $=\frac{-1}{2+1}x^{2+1}+\frac{2}{1+1}x^{1+1}+8x$

    $=-\frac{1}{3}x^3+x^2+8x$

    $=(-\frac{1}{3}(4^3)+4^2+8(4))-(-\frac{1}{3}(-2^3)+(-2^2)+8(-2))$

    $=(-\frac{64}{3}+16+32)-(\frac{8}{3}+4-16)$

    $=-\frac{64}{3}-\frac{8}{3}+16+32-4+16$

    $=-24+60$

    $=36$

Semoga Bermanfaat

Salam Matematika

sumber : http://supermatematika.com yunidionisia.blogspot.com