Konsep Jarak Titik ke Titik
Untuk memahami konsep jarak antara dua titik, mari kita perhatikan dua masalah berikut.
Bangun berikut merepresentasikan kota-kota yang terhubung dengan jalan. Titik merepresentasikan kota dan ruas garis merepresentasikan jalan yangmenghubungkan kota.
Faisal berencana menuju kota C berangkat dari kota A. Tulis kemungkinan rute yang ditempuh Faisal dan tentukan panjang rute-rute tersebut. Rute manakah yang terpendek? Menurut pendapat kalian berapa jarak antara kota A dan C? Beri alasan untuk jawaban kalian.
Nah, untuk menjawab masalah di atas, kita akan membuat tabel kemungkinan rute yang bisa dilalui Faisal berikut ini.
Dari tabel di atas tampak bahwa rute terpendek dari Kota A ke Kota C adalah rute yang pertama: A → C sepanjang 30 km.
Jadi, jarak antara kota A dan kota C adalah panjang lintasan terpendek yang menghubungkan antara kota A dan C, yaitu rute A → C sepanjang 30 km. 
Diketahui dua lingkaran seperti pada gambar berikut. Titik A, B, C, D, dan E terletak pada lingkaran $L_1$ dan titik P, Q, R, S, dan T terletak pada lingkaran $L_2$. Ruas garis manakah yang mewakili jarak antara kedua lingkaran tersebut?
Nah, untuk menjawab pertanyaan di atas perlu kalian ketahui bahwa dalam geometri, jarak dua bangun didefinisikan sebagai panjang ruas garis terpendek yang menghubungkan dua titik pada bangun-bangun tersebut. Coba kalian perhatikan ruas garis-ruas garis yang menghubungkan dua titik pada lingkaran $L_1$ dan $L_2$, manakah ruas garis terpendek? Jika CR adalah ruas garis terpendek di antara semua ruas garis yang menghubungkan dua titik pada lingkaran tersebut, maka ruas garis CR disebut jarak antara lingkaran $L_1$ dan lingkaran $L_2$.
Nah, dari dua masalah di atas kita dapat menyimpulkan jarak antara dua titik seperti berikut ini.
Contoh 1.
Diketahui kubus ABCD.EFGH dengan panjang rusuk 20 cm.
Hitunglah jarak antara titik-titik berikut.
a. B ke F
b. A ke D
c. G ke H
d. A ke C
e. H ke B
f. G ke titik tengah AB
Jawab:
a. Jarak titik B ke F diwakili oleh panjang ruas garis (rusuk) BF. Jadi, jarak titik B ke F adalah 20 cm.
b. Jarak titik A ke D diwakili oleh panjang ruas garis (rusuk) AD. Jadi, jarak titik A ke D adalah 20 cm.
c. Jarak titik G ke H diwakili oleh panjang ruas garis (rusuk) GH. Jadi, jarak titik G ke H adalah 20 cm.
d. Jarak titik A ke C diwakili oleh panjang ruas garis AC. Ruas garis AC merupakan diagonal bidang alas ABCD.
Dari gambar di atas, kita perhatikan bahwa segitiga ABC adalah segitiga siku-siku di B. Berdasarkan Teorema Pythagoras diperoleh hubungan:
| $AC^2$ |
=$AB^2+BC^2$ |
(Teorema Pythagoras) |
| =$20^2+20^2$ | (panjang AB = BC = 20 cm) | |
| =$400+400$ | ||
| =$400\times2$ | ||
| $AC$ | =$\sqrt{400\times2}$=$20\sqrt{2}$ | $(\sqrt{400\times2}$=$\sqrt{400}\times\sqrt{2}$=$20\sqrt{2})$ |
Jadi, jarak titik A ke C adalah $20\sqrt{2}$ cm.
e. Jarak titik H ke B diwakili oleh panjang ruas garis HB. Ruas garis HB merupakan diagonal ruang kubus ABCD.EFGH.
Dari gambar di atas, kita perhatikan bahwa segitiga BDH adalah segitiga siku-siku di D. Ruas garis BD adalah diagonal bidang alas ABCD, sehingga BD = AC = 20√2cm (hasil perhitungan pada bagian d).
Perhatikan segitiga BDH, berdasarkan Teorema Pythagoras diperoleh hubungan:
| $HB^2$ | =$BD^2+DH^2$ | (Teorema Pythagoras) |
| =${20\sqrt{2}}^2+20^2$ | (panjang BD = $20\sqrt{2}$ DH = 20 cm) | |
| =$800+400$ | ||
| =$1200\times2$ | ||
| $HB$ | =$\sqrt{400\times3}$=$20\sqrt{3}$ | $(\sqrt{400\times3}$=$\sqrt{400}\times\sqrt{3}$=$20\sqrt{3})$ |
f. Misalkan P adalah titik tengah AB. Jarak titik G ke titik tengah AB diwakili oleh panjang ruas garis GP seperti ditunjukkan pada gambar berikut.
Dari gambar di atas, kita perhatikan bahwa segitiga BGP adalah segitiga siku-siku di B. Ruas garis BG adalah diagonal bidang alas BCGF, sehingga BG = $20\sqrt{2}$ cm (panjang BG = AC = BD, semuanya adalah diagonal bidang kubus ABCD.EFGH).
Perhatikan segitiga BGP, berdasarkan Teorema Pythagoras diperoleh hubungan:
| $GP^2$ $GP$ | =$BG^2+BP^2$ =${20\sqrt{2}}^2+10^2$ =$800+100$ =$900$ =$\sqrt{900}$=30 | (Teorema Pythagoras) (panjang BD = $20\sqrt{2}$ DH = 20 cm) |
Jadi, jarak titik G ke P titik tengah AB adalah 30 cm.
Contoh 2.
Andi mempunyai kamar tidur yang berukuran 3m × 3m × 4m. Tepat di tengah plafon kamar Andi dipasang lampu. Jika saklar lampu diletakkan tepat di tengah salah satu dinding kamar, berapakah jarak dari lampu ke saklar?
Jawab:
Kamar Andi berukuran 3m × 3m × 4m, berarti panjang kamar 3 m, lebar 3 m, dan tinggi 4 m.
Jarak antara lampu dan saklar dapat diilustrasikan seperti gambar berikut.
Misalkan lampu (L), saklar (S) berada di dinding ADHE, dan P adalah titik tengah EH.
Jarak antara lampu dan saklar adalah LS.
Panjang ruas garis PS = $\frac{1}{2}$AE=$\frac{1}{2}$(4 m)=2 m.
Panjang ruas garis PL = $\frac{1}{2}$EF=$\frac{1}{2}$(3 m)=$\frac{3}{2}$ m.
Perhatikan segitiga LPS siku-siku di P, berdasarkan Teorema Pythagoras diperoleh hubungan:
| $LS^2$ $LS$ | =$LP^2+PS^2$ =${\frac{3}{2}}^2+2^2$ =$\frac{9}{4}+4$ =$\frac{9}{4}+\frac{16}{4}$ =$\frac{25}{4}$ =$\sqrt{\frac{25}{4}}$=$\frac{5}{2}$=2,5 | (Teorema Pythagoras) (panjang LP = $\frac{3}{2}$m dan rusuk PS = 2 m) |
Jadi, jarak titik G ke P titik tengah AB adalah 2,5 m.
Jadi, Panjang kabel terpendek yang diperlukan Andi untuk menghubungkan lampu dan saklar adalah 2,5 meter.
Contoh 3
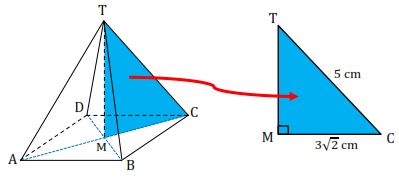
Diketahui limas T.ABCD seperti pada gambar di bawah. ABCD merupakan persegi dengan panjang rusuk 6 cm. TA = TB = TC = TD = 5 cm dan M adalah titik tengah AC.
Hitung jarak antara titik T dan titik M.
Jawab:
Perhatikan segitiga ABC, siku-siku di B, berarti:
| $AC^2$ $LS$ | =$AB^2+BC^2$ =$6^2+6^2$ =$36+36$ =$36\times2$ =$\sqrt{36\times2}$=$6sqrt{2}$ | (Teorema Pythagoras) (panjang LP = $\frac{3}{2}$m dan rusuk PS = 2 m) |
Titik M adalah titik tengah AC, sehingga AM = CM = $\frac{1}{2}$AC=$\frac{1}{2}6\sqrt{2}$=$3\sqrt{2}$cm
| $TC^2$ $TM^2$ $LS$ | =$CM^2+TM^2$ =$TC^2-CM^2$ =$5^2-{3\sqrt{2}}^2$ =$25-18$ =$7$ =$\sqrt{7}$ | (Teorema Pythagoras) (panjang TC = 5 cm dan CM = $3\sqrt{2}$) |
Jadi, jarak antara titik T dan titik M adalah $\sqrt{7}$ cm yang merupakan tinggi dari limas T.ABCD.
Latihan
1. Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Hitunglah jarak antar titik-titik berikut.
a. titik A dan G
b. titik D dan F
c. titik B dan titik tengah garis EG
d. titik E dan titik tengah garis BG
2. Diketahui limas beraturan P.QRST dengan panjang RS = 8 cm dan PR = 12 cm, seperti pada gambar.
Dengan menggunakan Teorema Pythagoras, hitung jarak antar titik berikut.
a. titik P dan titik tengah RS
b. titik P dan titik perpotongan QS dan RT
3. Diketahui limas beraturan T.ABC dengan bidang alas berbentuk segitiga sama sisi. TA tegak lurus dengan bidang alas. Jika panjang AB = 4$\sqrt2$ cm dan TA = 4 cm, tentukan jarak antara titik T dan C.
4. Perhatikan limas segi enam beraturan berikut.
Diketahui panjang AB = 10 cm dan TA = 13 cm. Titik O merupakan titik tengah garis BE. Tentukan jarak antara titik T dan titik O.
5. Perhatikan bangun berikut ini.
Jika diketahui panjang AB = 5 cm, AE = BC = EF = 4 cm, maka tentukan:
a. Jarak antara titik A dan C
b. Jarak antara titik E dan C
c. Jarak antara titik A dan G
6. Diketahui balok ABCD.EFGH dengan panjang rusuk AB = 8 cm, BC = 6 cm, dan AE = 9 cm. Titik M merupakan titik potong antara diagonal AC dan BD. Rusuk CG diperpanjang 3 cm, kemudian dari titik M ditarik garis miring sehingga memotong perpanjangan rusuk CG di titik N. Hitung panjang ruas garis MN yang terjadi dan buat sketsa permasalahan tersebut.
7. Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P, Q, dan R berturut-turut terletak pada pertengahan garis AB, BC, dan bidang ADHE. Tentukan jarak antar titik berikut.
a. titik P ke titik R
b. titik Q ke titik R
8. Pada gambar di bawah menunjukkan piramida terpotong ABCD.EFGH tegak beraturan dengan ABCD dan EFGH merupakan persegi yang saling sejajardengan AB = 12 cm, EF = 8 cm, dan AE = BF = CG = DH = 10 cm.
Hitung jarak antar titik.
a. E dan G
b. A dan C
c. titik potong diagonal HF dan EG dengan titik potong AC dan BD.
Pembahasan
sumber : @2020, Direktorat SMA, Direktorat Jenderal PAUD, DIKDAS dan DIKMEN
