Konsep Jarak Titik ke Garis
Pada gambar di bawah, titik A terletak di luar garis g. Bagaimana menentukan jarak antara titik A dan garis g?
Coba kalian ingat kembali materi jarak titik ke titik pada Kegiatan Pembelajaran 1, yaitu jarak titik ke titik adalah panjang ruas garis terpendek yang menghubungkan titik-titik tersebut.
Nah, jika kita ingin mencari jarak antara titik A ke garis g, maka kita perlu membuat sebuah titik yang terletak di garis g, lalu menarik sebuah ruas garis terpendek dari titik A ke titik pada garis g tersebut.
Manakah ruas garis terpendek? Tentunya ruas garis terpendek adalah ruas garis AB yang tegak lurus (membentuk sudut siku-siku) dengan garis g. Mengapa demikian?
Coba kalian perhatikan ruas garis AB dan AC. Terlihat bahwa ABC membentuk segitiga siku-siku di B dengan AC merupakan sisi miring. Nah, tentunya kalian masih ingat bahwa sisi miring merupakan sisi terpanjang pada sebuah segitiga siku-siku. Ini berarti bahwa ruas garis AB lebih pendek dari AC.
Demikian halnya jika kita membuat ruas garis lainnya dari A ke garis g, misalnya AD. Tentunya akan terbentuk segitiga ABD siku-siku di B dengan AD merupakan sisi miring. Berarti AD pun lebih panjang dari AB, dan demikian seterusnya.
Jadi, ruas garis terpendek adalah ruas garis AB. Dengan demikian dapat kita simpulkan bahwa jarak titik A ke garis g adalah panjang ruas garis AB, yaitu ruas garis tegak lurus antar titik A ke garis g.
Dalam hal ini, titik B biasa disebut sebagai proyeksi titik A terhadap garis g.
Pengertian Jarak Titik ke Garis
Prosedur Menghitung Jarak Titik ke Garis
Langkah-langkah untuk menghitung jarak titik A ke garis g sebagai berikut.
a. Hubungkan titik A ke titik C dan titik D sehingga terbentuk segitiga ACD.
b. Hitung jarak antar dua titik, yaitu AC, AD, dan CD untuk menetapkan jenis segitiga.
c. Hitung tinggi segitiga ACD, yaitu AB yang merupakan jarak titik A ke garis g.
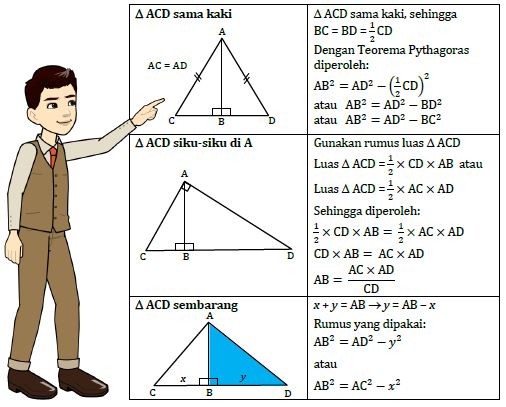
Dari langkah-langkah di atas, ada 3 jenis segitiga ACD yang mungkin terbentuk. Berikut ini cara menghitung panjang ruas garis AB atau jarak titik A ke garis g.Contoh 1.
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Berapakah jarak titik A ke diagonal bidang BE?
Jawab:
Perhatikan gambar.
Jika titik B dan E dihubungkan dengan ruas garis, maka diperoleh,
Jarak titik A ke bidang diagonal BE adalah panjang ruas garis AM dengan BM = 12BE, karena segitiga ABE merupakan segitiga sama kaki (AB = AE).
Dengan menggunakan Teorema Pythagoras diperoleh,
$AM^2=AB^2-BM^2$
Terlebih dulu ditentukan panjang BE. Dengan menggunakan Teorema Pythagoras diperoleh,
| $BE^2$ | $=AB^2+AE^2$ |
| $=6^2+6^2$ | |
| $=36\times2$ | |
| $BE$ | $=\sqrt{6^2\times2}=6\sqrt{2}$ |
Sehingga panjang $BM =\frac{1}{2}BE= \frac{1}{2}(6\sqrt{2})=3\sqrt{2}$.
Dengan demikian diperoleh,
| $AM^2$ | $=AB^2-BM^2$ |
| $=6^2-(3\sqrt{2})^2$ | |
| $=36+18$ | |
| $=54$ | |
| $BE$ | $=\sqrt{54}=\sqrt{9\times6}=3\sqrt{6}$ |
Catatan:
Contoh 2.
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Hitunglah jarak titik H ke garis AG.
Jawab:
Perhatikan gambar. Titik N terletak pada garis AG, dan ruas garis HN tegak lurus garis AG.
Pada gambar di atas terlihat $\Delta$ AHG siku-siku di H dan garis tinggi HN.
Berdasarkan Teorema Pythagoras, AH merupakan diagonal bidang kubus berarti $AH = 8\sqrt{2}$ cm dan AG merupakan diagonal ruang kubus, berarti $AG = 8\sqrt{3}$ cm.
Kita akan menghitung luas $\Delta$ AHG dalam dua sudut pandang, yaitu
Luas $\Delta$ $AHG = \frac{1}{2} \times AH \times GH$ atau Luas $\Delta$ $AHG = \frac{1}{2} \times AG \times HN$
Sehingga diperoleh,
| $\frac{1}{2}AH \times GH$ | $=\frac{1}{2}AG \times HN$ |
| $8\sqrt{2}\times 8$ | $=8\sqrt{3}\times HN$ |
| $HN$ | $=\frac{8\sqrt{2}\times8}{8\sqrt{3}}$ |
| $HN$ | $=\frac{8\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$ |
| $HN$ | $=\frac{8}{3}\sqrt{6}$ |
Contoh 3.
Diketahui limas beraturan T.ABCD, panjang rusuk AB = 3 cm dan TA = 6 cm. Tentukan jarak titik B ke rusuk TD.
Jawab:
Misal P proyeksi titik B ke ruas garis TD.
Jarak titik B ke rusuk TD adalah BP. Perhatikan bidang alas ABCD dengan panjang rusuk 3 cm. Dengan Teorema Pythagoras diperoleh
| $BD^2$ | $=AB^2+AD^2$ |
| $=3^2+3^2$ | |
| $=9\times2$ | |
| $BD$ | $=\sqrt{9\times2}=3\sqrt{2}$ |
Dengan Teorema Pythagoras, tinggi limas TO adalah

Jadi, jarak titik B ke rusuk TD adalah $\frac{3}{2}\sqrt{7}$ cm.
Kembali ke Kelas Online
| $TO^2$ | $=TB^2-OB^2$ |
| $=6^2-(\frac{3}{2})^2$ | |
| $=36-\frac{9}{2}=\frac{63}{2}$ | |
| $TO$ | $=\sqrt{\frac{63}{2}}=\sqrt{\frac{9\times7}{2}\times\frac{2}{2}}=\frac{3}{2}\sqrt{14}$ |

Perhatikan segitiga TBD.
Kita akan menghitung luas $\Delta$ TBD dalam dua sudut pandang, yaitu
Luas $\Delta$ $TBD = \frac{1}{2} \times BD \times TO$ atau Luas $\Delta$ $TBD = \frac{1}{2} \times TD \times BP$
Sehingga diperoleh,
| $\frac{1}{2}BD \times TO$ | $=\frac{1}{2}TD \times BP$ |
| $BP$ | $=\frac{BD \times TO}{TD}$ |
| $BP$ | $=\frac{3\sqrt{2}\times\frac{3}{2}\sqrt{14}}{6}$ |
| $BP$ | $=\frac{\frac{9}{2}\sqrt{28}}{6}=\frac{\frac{9}{2}\sqrt{4\times7}}{6}=\frac{9\sqrt{7}}{6}=\frac{3}{2\sqrt{7}}$ |
Jadi, jarak titik B ke rusuk TD adalah $\frac{3}{2}\sqrt{7}$ cm.
sumber : @2020, Direktorat SMA, Direktorat Jenderal PAUD, DIKDAS dan DIKMEN